








There are two major differences between qubits.
There is an ensemble qubit which contain a large number of particles that together act as a single qubit and there is what one typically thinks of as a qubit, which is a single particle or material.
Possible qubits include single photons, trapped atomic ions, neutral atoms, nuclear spins, quantum dots, impurities in silicon and diamond, etc...

REQUIREMENTS OF A QUBIT
Currently researchers are testing a variety of materials as possible qubits for quantum computing. The key considerations when evaluating a qubit is whether it is scalable, capable of accessing universal logic, and whether it is correctable. These ideas have been identified here and will be summarized in the paragraphs that follow.
SCALABILITY
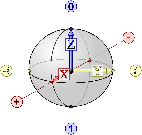
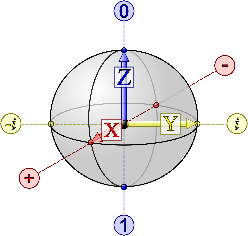
A qubit is a binary quantum system that can be measured as either a |0> or a |1>. To be scalable, there must be a large number of qubits, which the operator must be able to interact with - and which should be able to interact with each other when the operator wishes. This will allow the operator to have access to a larger logic space [known as SU(2^N)].
Alternatively a quantum computer can have a large logic space if it is implemented with qudits (a qubit is a system which lives in a two-dimensional Hibert space, since it has access to only two states, while a qudit has access to a higher order, d-dimensional Hilbert space).
This equivalently would allow a larger logic space, but instead between energy levels.
UNIVERSAL LOGIC
Above we mentioned that universal logic gates will allow a quantum computer to perform any logical operation. It is also important that the quantum gates are able to be implemented fault-tolerantly.

QUANTUM QUBITS
CORRECTABILITY
The operator must be able to correct the state of the quantum computer to manage the qubit’s state. What good is a quantum computer without error-correction?
Here are couple of examples of when this is necessary:
STATE INITIALIZATION:
Systems always tend towards the lowest possible energy. This causes qubits to thermalize to an equilibrium state. However, when beginning a quantum algorithm, it is often important to initialize the qubits to a known state. It is also important for the qubit to be in the state that the user needs the algorithm to begin at. There will almost always be an associated error with the initialized state.
MEASUREMENT:
Systems must be able to quickly measure the state of a system accurately. Interestingly, measurement can act as a replacement for state initialization since a quantum measurement alters the qubit state. In the case of a projection measurement for instance, the qubit's state is projected onto a measured state, which could be used as an initial state for a quantum algorithm. However there obviously must always be a read-out for the system, so a quantum komputer must be capable of quantum measurements.
CAN YOU GIVE ME ANY EXAMPLES OF A QUBIT?
Can you show me some examples of a qubit?
Well, to begin with, there are two major differences between qubits:
- There is an ensemble qubit which contain a large number of particles that together act as a single qubit.
- And there is what one often thinks of as a qubit, which is a single particle or material.
There are an near-infinite amount of possible qubits. Really, just about anything could theoretically act as a quantum-qubit. As long as it exists in a quantum state and can be measured.
Possible qubits would include single photons, trapped atomic ions, neutral atoms, nuclear spins, quantum dots, impurities in silicon and diamond, superconducting qubits, and others. Each technology has its own tradeoffs. Additionally, methods of applying and implementing qubits differ drastically, depending on the type of qubit involved. Therefore, in the future, it will be possible to have hardware and software tailor-made to work best with your specific flavor of qubit! Potentially drastically-increasing processing speed in the process! That’s just one of the potential game-changing benefits of quantum-computers and quantum-computing. There are lots more...
When performing a logical operation, there will likely be an error associated with it. For quantum computing it is appears to be generally accepted that error probabilities should be on the order of 0.0001 or lower.
Minimizing this error is key especially when a large number of gates are sequentially applied to a given qubit. It is important to find a universal set of gates that collectively has the smallest error probability since each gate has a different error probability associated with it.












